白矮星为什么存在质量上限?为什么计算白矮星内部压强需要使用狭义相对论?9月3日12时,《张朝阳的物理课》第一百七十期开播,搜狐创始人、董事局主席兼CEO、物理学博士张朝阳坐镇搜狐视频直播间,在简单复习上次直播课介绍的内容后,指出了上次直播课的计算所忽略的狭义相对论因素,导致计算的电子简并压过大。
在考虑狭义相对论的情况下,张朝阳类比薛定谔方程给出了相对论性粒子的克莱恩-高登方程,并由此得知在非相对论情况下的电子k空间的结论仍然使用,只需要修改压强公式即可。随后,他计算了相对论情况下的电子简并压,并与维持白矮星平衡的所需压强做对比,最终得到了白矮星的质量上限。

为什么计算白矮星内部压强需要考虑相对论效应
在上一次物理直播课中,张朝阳估算了平衡状态下的白矮星中心压强,结果为
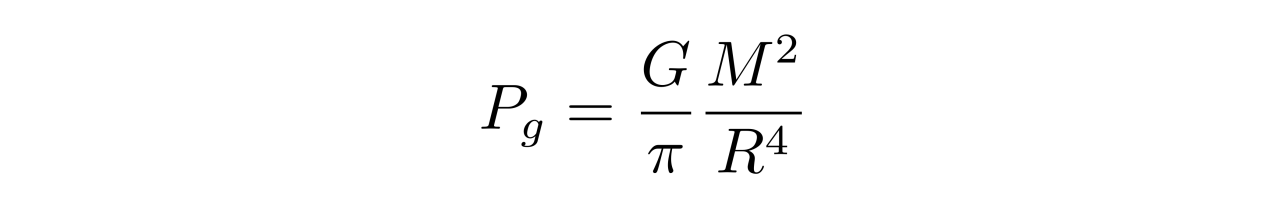
其中,G是万有引力常数,R是白矮星半径,M是白矮星总质量。同时,张朝阳还估算了一定质量与半径的情况下的白矮星中心处电子简并压为
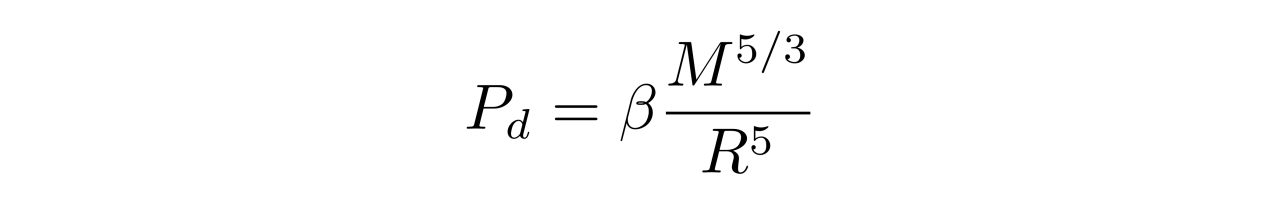
其中β是一个与M、R无关的常数。
在上次直播课中,张朝阳分析得知白矮星会平衡在满足Pg=Pd的半径R0处。从这前面两个结果可以看到,当M保持固定时,Pd随着R的增大会下降得比Pg快,因此当R足够大时,Pd会小于Pg;另一方面,当R趋向于0时,Pd将会大于Pg。因此,在压强-半径坐标系上,Pd与Pg曲线必定相交,如下图所示:
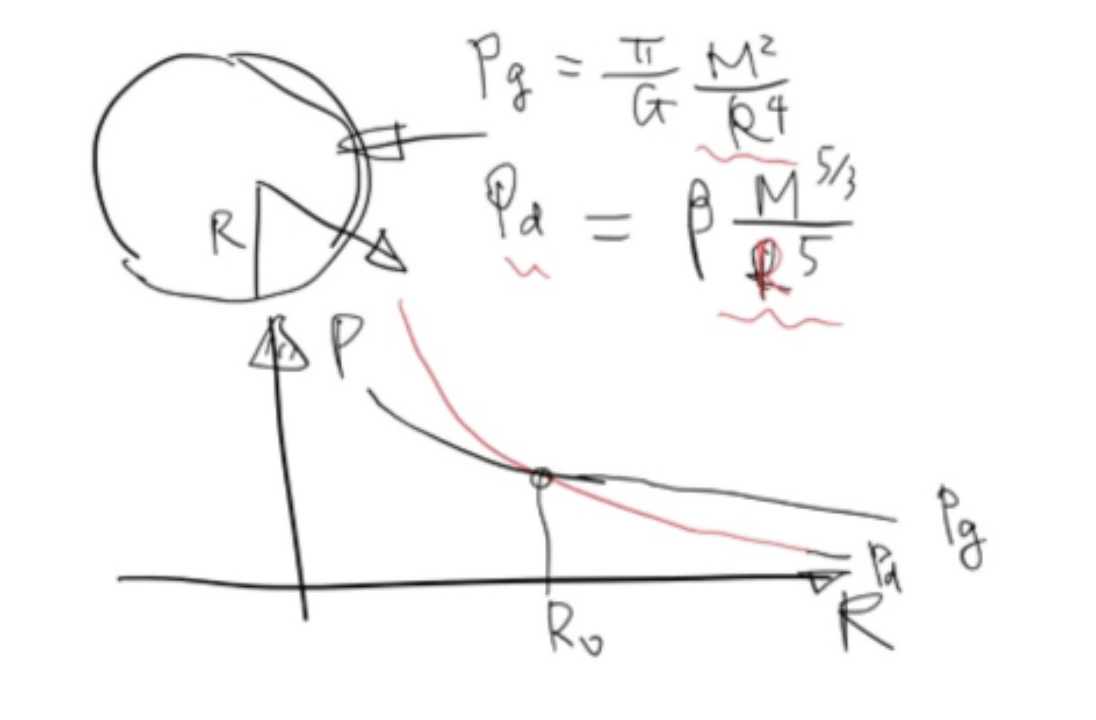
如果忽略电子与质子的反应,那么Pd与Pg曲线相交意味着无论质量多大,白矮星最终都可以稳定平衡存在。但是,现实中白矮星存在一个质量上限,这个质量上限就是钱德拉塞卡极限,大约是1.44倍太阳质量。
根据上一次直播课的分析,当白矮星质量为一个太阳质量时,电子所占据的空间尺度大约在1500fm,这个尺度下电子很难与质子反应变成中子和中微子。根据同样的分析,当白矮星质量是1.44个太阳质量时,电子所占据的尺度大约在1200fm,这个尺度依然很难让电子和质子反应。那么,到底是什么原因导致了白矮星的质量上限呢?
张朝阳提示,事实上在计算电子气体时没有考虑相对论效应。因为电子气体的压强本质上是电子对容器壁的碰撞所导致的力的现象。在同样的动量大小下,碰撞粒子数越多,所表现出来的压强越大。
但是,碰撞频率正比于粒子速度,而在相对论的情况下,因为粒子质量变大了,所以具有特定动量的粒子所对应的速度是小于牛顿力学情况下的具有相同动量的粒子所对应的速度的,因此在相同动量情况下,用牛顿力学来计算的粒子碰撞频次高于用相对论来计算的碰撞频次,最终就会导致用牛顿力学计算出来的压强偏大。
后面会知道,如果考虑(极端)相对论情形的话,Pd与R的关系为
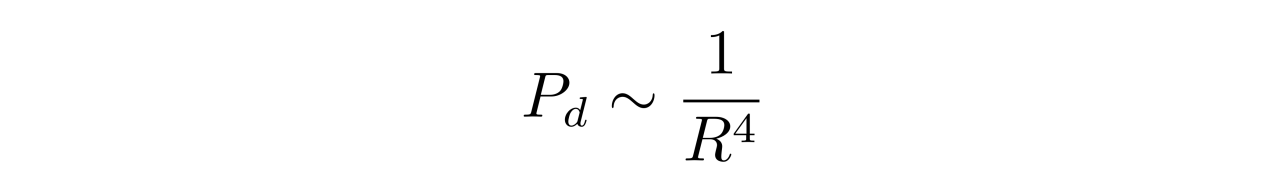
先不考虑白矮星是否处于平衡状态,那么在相同质量下,白矮星的半径越小,其内部电子气体的密度越大,从而费米能越高。因此,半径越小,越偏离牛顿力学,从而也越接近于极端相对论给出来的结果。
换言之,上式在R越小的时候符合得越好。在R趋向于零时,Pg正比于1/R^4,Pd也正比于1/R^4,这就导致了在压强-半径坐标系上,Pg曲线与Pd曲线可能没有交点,特别是当Pg大于Pd时,无论怎么压缩白矮星,电子气体都无法提供足够的简并压来抵抗引力压缩,于是白矮星会被无限压缩。
当然,实际情况并不会被无限压缩,因为当白矮星被压缩到一定程度后,电子与质子会发生反应,白矮星会变成中子星,这时候就得看中子简并压能否抵抗引力压缩了。
引入克莱恩-高登方程 分析k空间的异同
为了计算相对论情形的电子气体压强,需要先知道自由的相对论粒子其波函数满足的方程。回忆薛定谔方程的“导出”过程,动量与能量作如下替换:
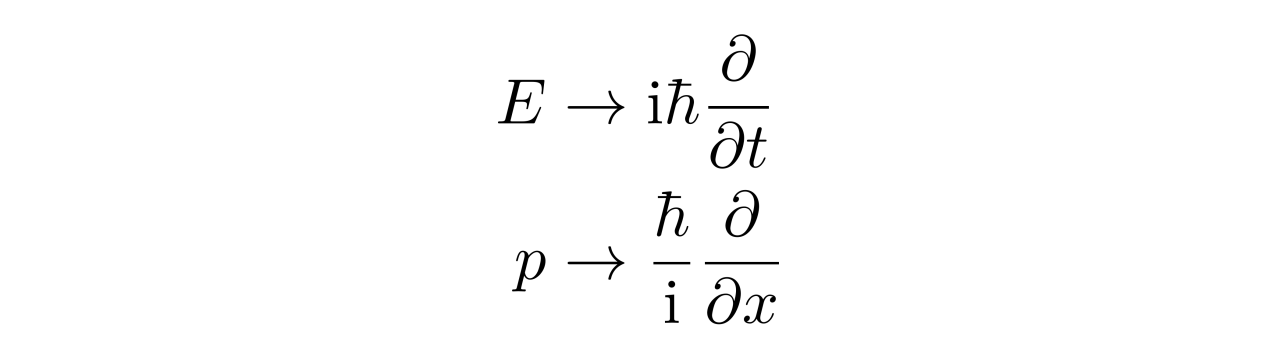
再根据牛顿力学中的动能表达式

就会得到自由粒子的薛定谔方程:
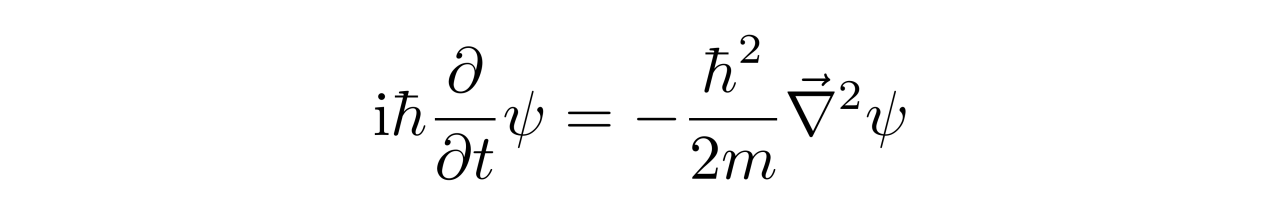
如果考虑相对论的能量动量关系
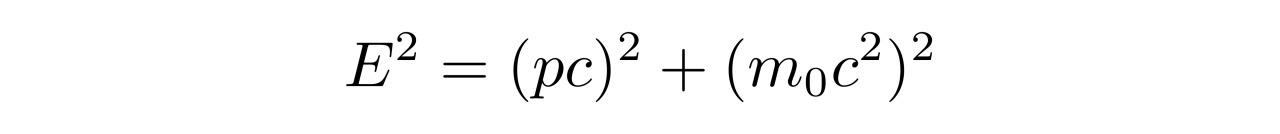
那么会得到如下方程:

移项并化简可得
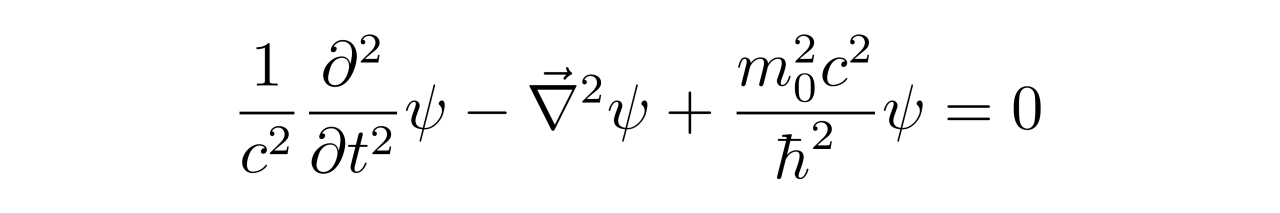
这就是相对论性自由粒子所需要满足的方程,被称为克莱恩-高登方程。虽然有自旋的自由粒子的基本方程不是克莱恩-高登方程,但是都能退化回克莱恩-高登方程,因此克莱恩-高登方程是一个普遍成立的方程。如果粒子的静止质量为零,那么上述方程就会回到以前介绍过的波动方程:
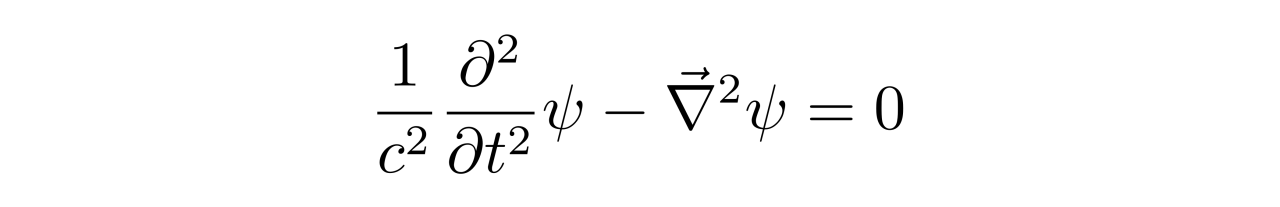
克莱恩-高登方程的平面波解为
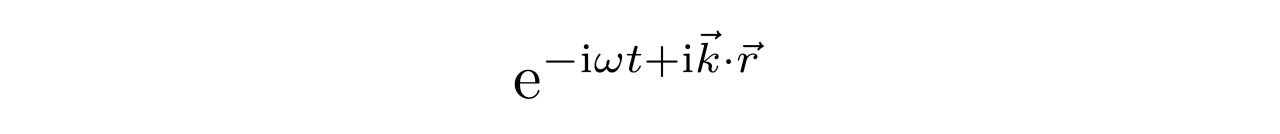
将其代入方程,可知ω和k需要满足
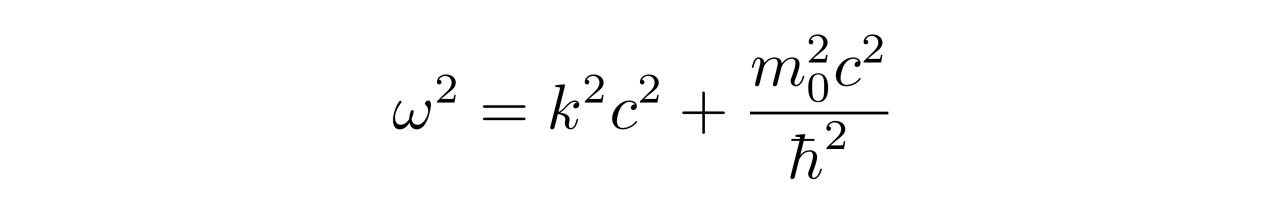
上式中的k是矢量k的大小。从前面能量E和动量p的替换关系可以知道,此平面对应的能量与动量分别为
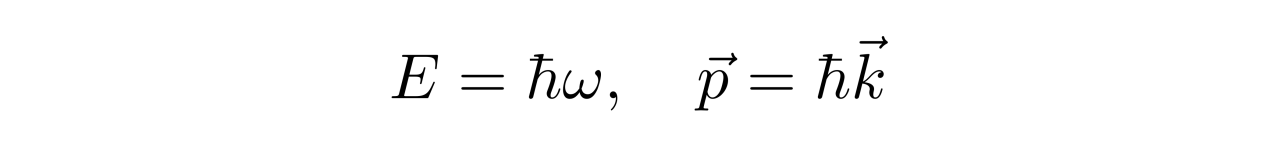
于是,由前一式子可以得到

这正是相对论性粒子的能量与动量所满足的关系。
 (张朝阳介绍克莱恩-高登方程及其平面波解)
(张朝阳介绍克莱恩-高登方程及其平面波解)
如果考虑无限深势阱,求解克莱恩-高登方程的话依然会得到如下形式的解
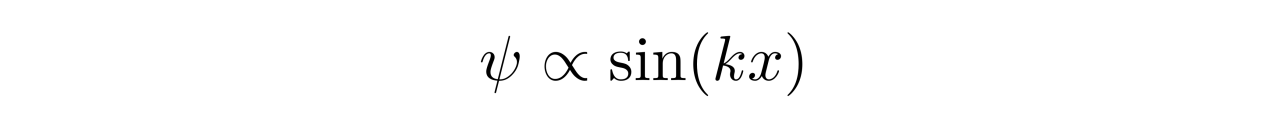
因此,相对论性自由电子的k空间与非相对论情形的k空间是一样的,因此在计算电子总数以及电子压强时,都是对同样的k空间中的1/8球体进行积分。唯一不一样的地方是,如果涉及到能量了,就需要考虑如下的关系:
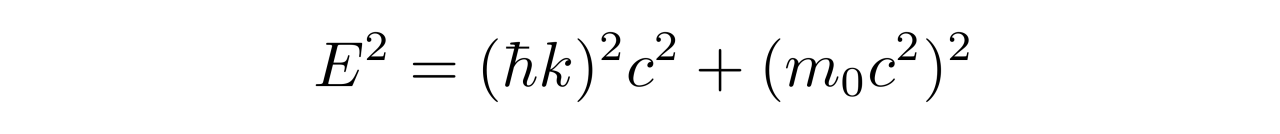
计算相对论性电子气体压强 分析得到钱德拉塞卡极限
即使在相对论情形下,单位面积单位时间内电子碰撞容器壁导致的动量改变都表现为压强。与非相对论情形类似,单位时间内碰撞容器壁(设面积为A)所导致的动量改变为
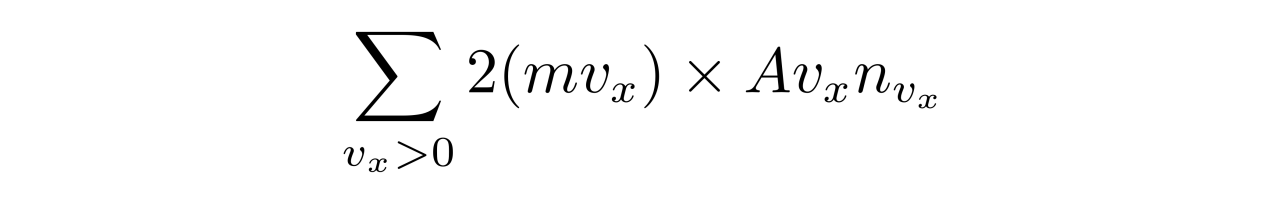
上式假设了容器壁垂直于x轴并与y轴重合,电子分布在x轴负方向那一侧,因此需要v_x>0的电子才能碰上这块容器壁。n_{v_x}是速度的x分量为v_x的电子数密度。上式的求和在必要的情况下需要理解为积分。
对于压强,只需要将上式除以A即可得到。由于速度分布在正负方向是一样的,因此有
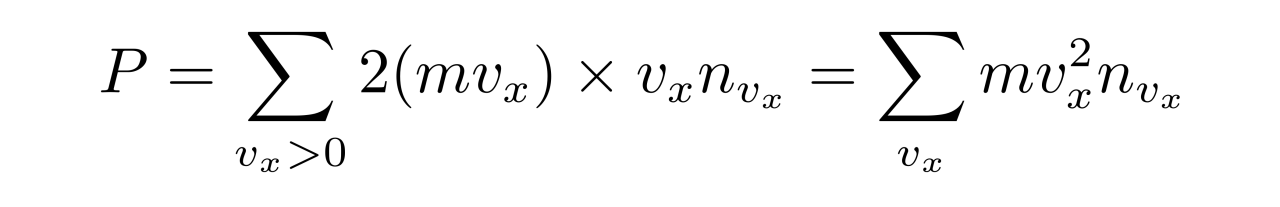
在相对论情况下,电子质量会依赖于速度大小v:
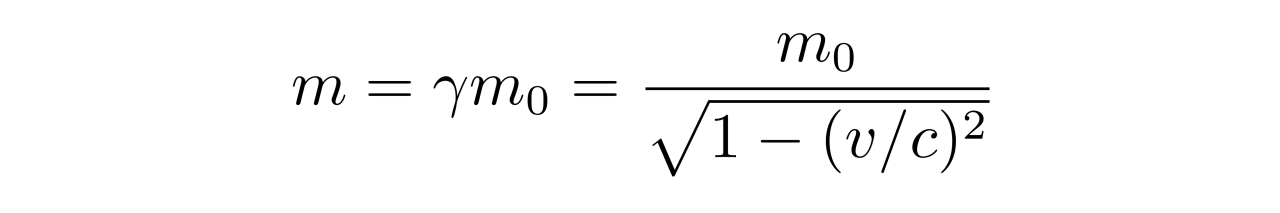
因此,质量m不仅依赖于v_x,还依赖于v_y、v_z,因此前面关于压强的表达式应该写为

另一方面,根据动量p与k的关系,有
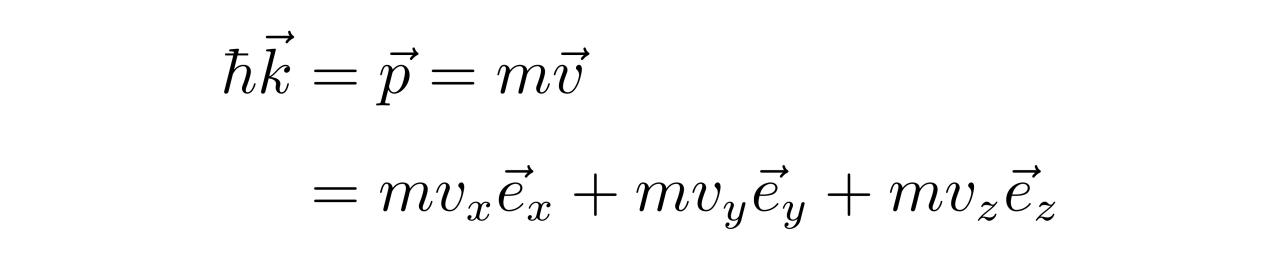
因此有
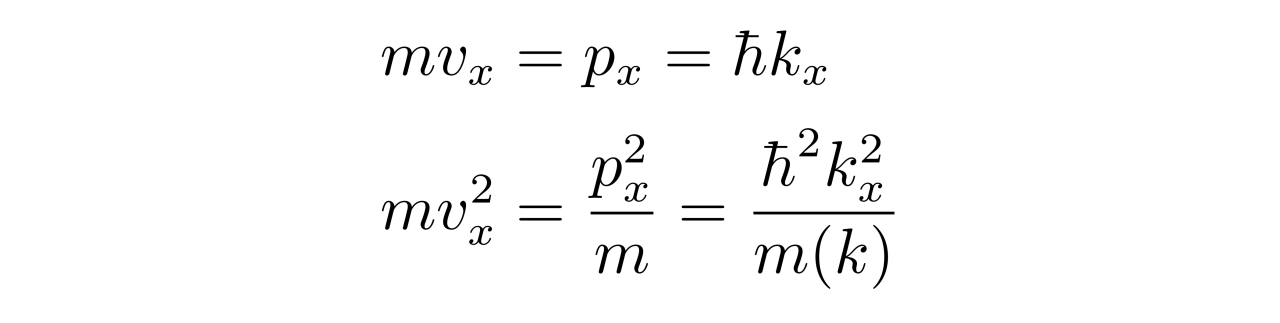
考虑到v_x与k_x的关系,借助以前在k空间上的分析,可以知道n_{v_x}为
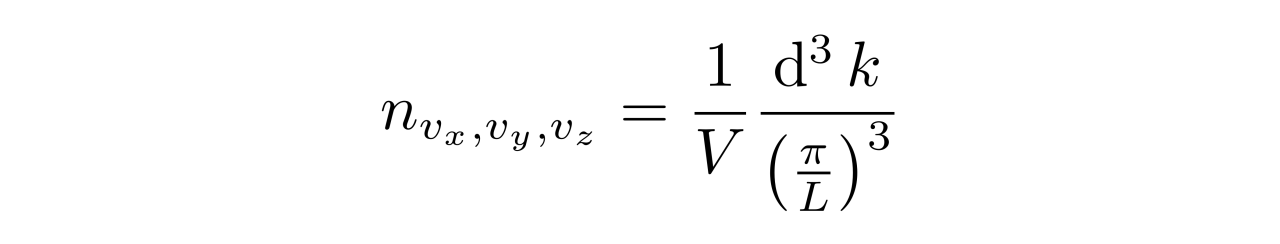
其中L是立方形容器的边长,V=L^3是容器体积。由此可得压强为

上式第一行等号右边的因子2来源于电子自旋的两个自由度,因子1/8来源于k空间的1/8球体。
考虑到空间各向同性,上式可以改写为
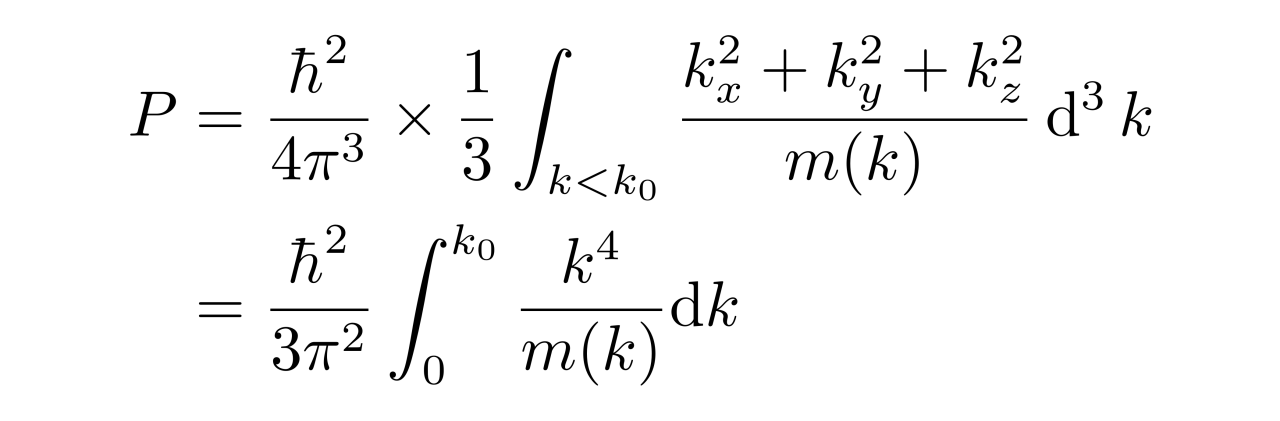
上式第二行将直角坐标的积分换成了球坐标下的积分,并将角度部分积分出来了。
根据质能关系,有
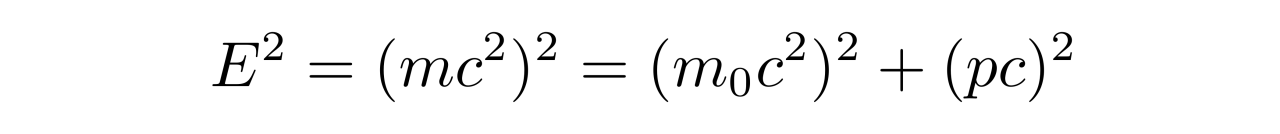
由此可得

所以

令a=m0*c/ℏ,借助积分公式
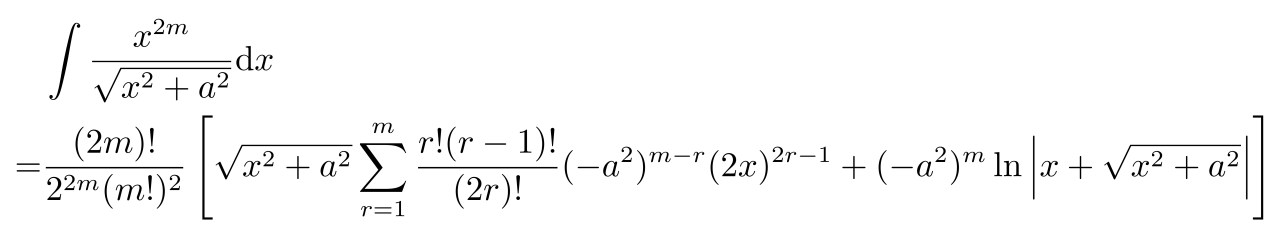
可得
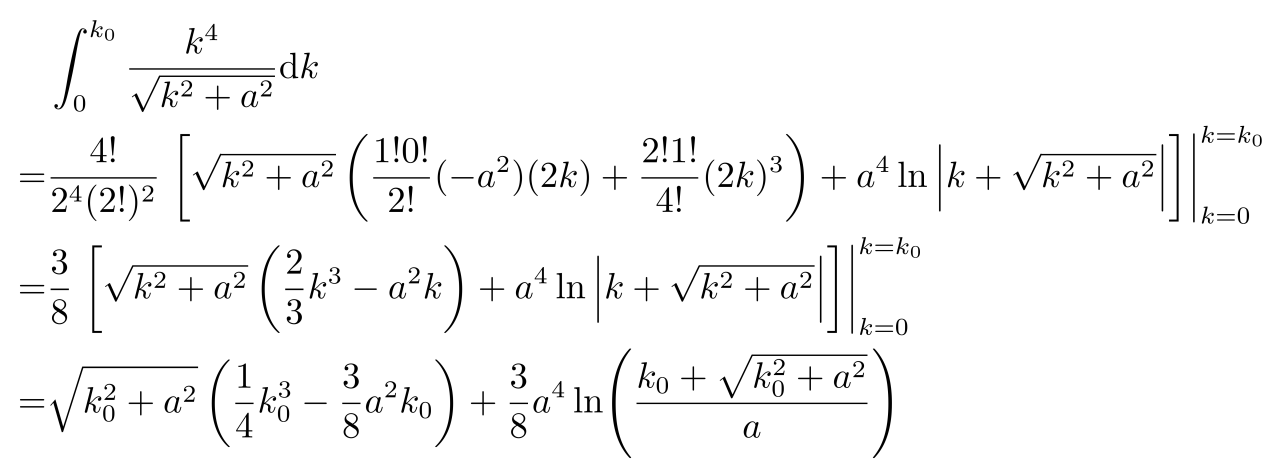
由于考虑的是白矮星半径趋向于零的情况(暂不管白矮星是否处于平衡状态),此时电子气体的密度很大。根据之前的直播课,知道
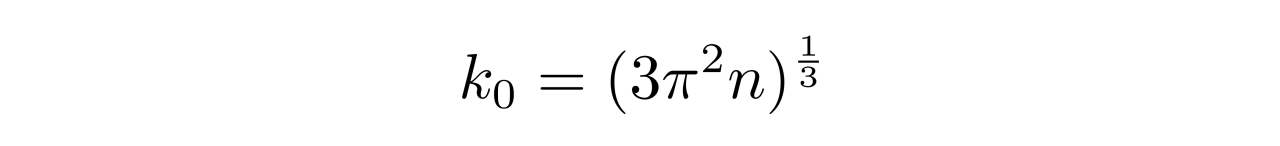
可见,当白矮星半径趋向于零时,k0可以取到非常大的值,这时候k0将远远大于a(这种情况就对应着极端相对论的情况)。这样的话,前面的积分结果中的显著项是k0的最高次项,于是
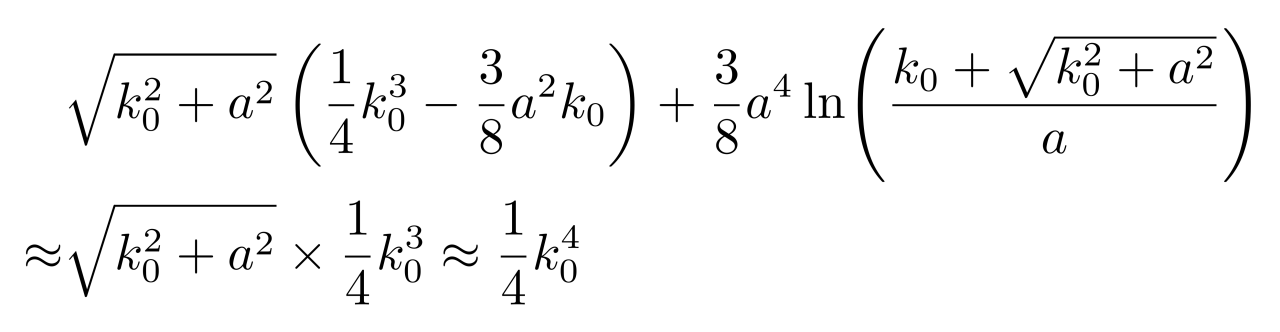
所以,得到
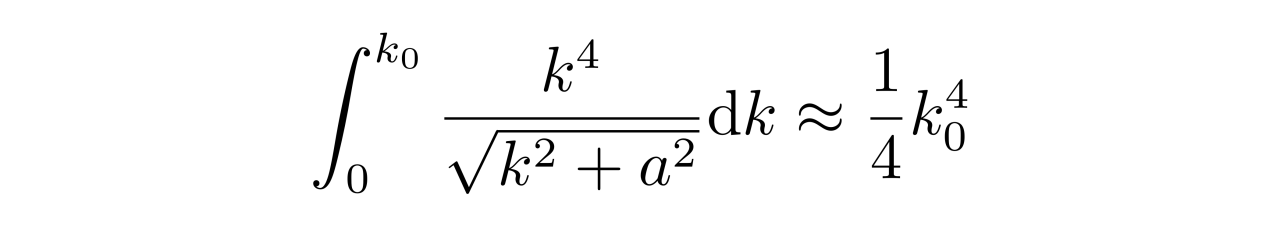
于是,在极端相对论的情况下,电子气体的压强为
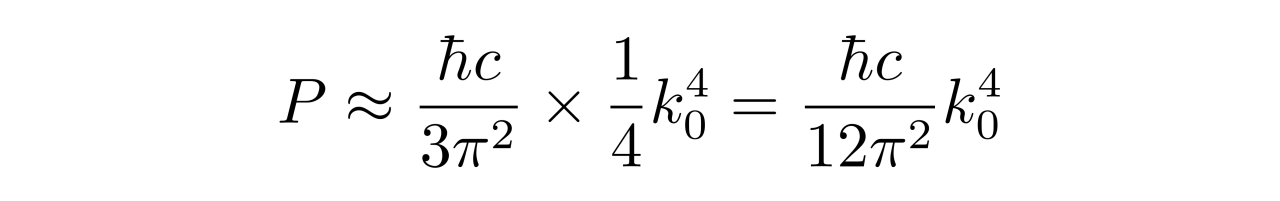
考虑到
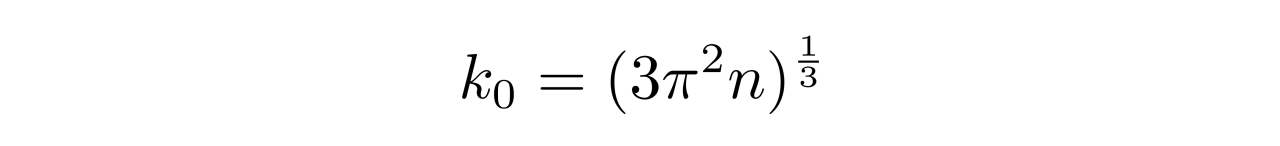
于是
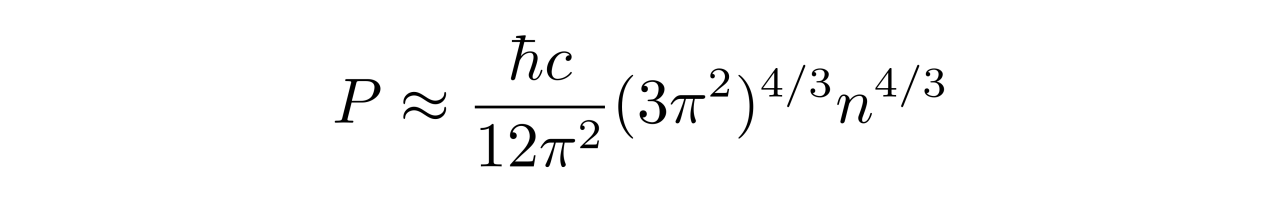
根据上一次直播课的推导,白矮星中心处的电子数密度约为
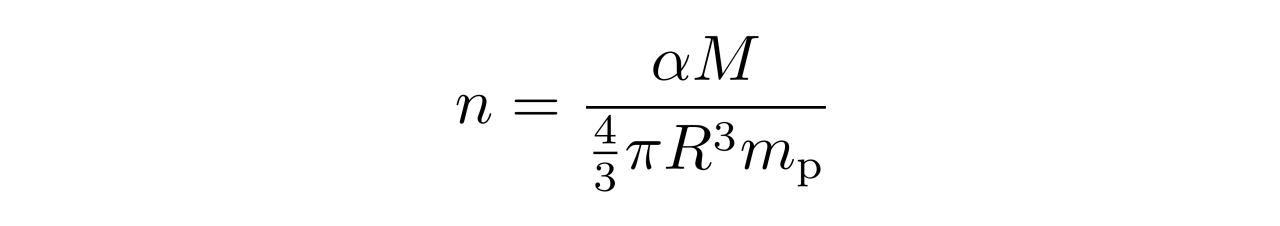
其中α是上一次直播课介绍的系数,可以取为2,m_p是质子质量。将其代入前面的压强公式,可以得到白矮星中心处的电子简并压为
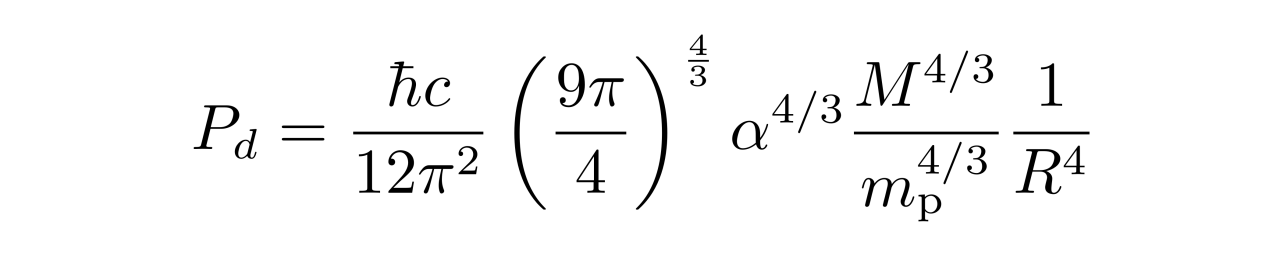
需要强调的是,因为前面使用了k0远大于a这个近似条件,所以这个式子只在R很小的时候才成立,它表示的是在质量M保持固定时,半径R趋向于0时白矮星中心处的电子简并压的变化情况。
对于R比较大的时候,k0远大于a这个条件不再成立。特别的是,当R很大时,电子数密度n很小,这时候电子气体退化成非相对论电子气体,其简并压满足的是正比于1/(R^5)的关系。将这里的讨论总结起来就是:

而不管R是大还是小,维持白矮星平衡所需的中心压强都是
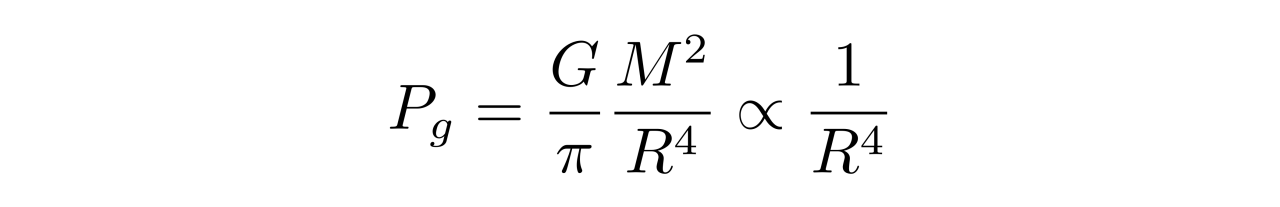
如果在R比较小的时候,Pg小于Pd,当R变大之后,Pd先以1/(R^4)的速度下降,然后以1/(R^5)的速度下降,而Pg保持以1/(R^4)的速度下降,最终Pd必小于Pg,因此在压强-半径坐标系上,Pd与Pg曲线必定相交,这样的话白矮星能够维持平衡,平衡点就对应着Pd与Pg曲线交点。
如果在R比较小的时候,Pg大于Pd,当R变大之后,Pd先以1/(R^4)的速度下降,然后以1/(R^5)的速度下降,Pg保持以1/(R^4)的速度下降,可见Pg曲线永远在Pd曲线上方,它俩没有相交点(如下图所示),因此无论半径为多少,电子简并压都无法提供足够的压强抵抗白矮星塌缩。
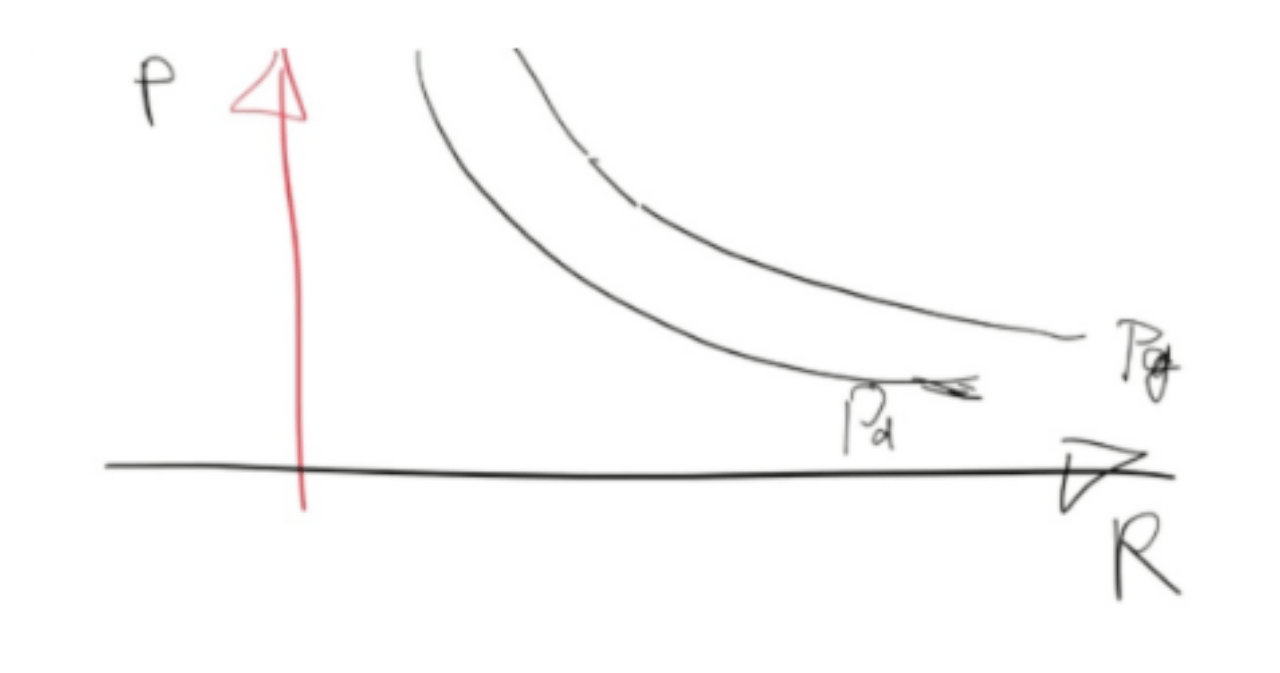
从前面的结果可以看到,在R足够小时,Pd正比于M^{4/3},Pg正比于M^2,因此当M增大时,同一个R下的Pg增长速度大于Pd的增长速度。因此,只要M足够大,Pg将会大于Pd,于是这个质量对应的白矮星将无法稳定存在。那白矮星的临界质量是多少呢?临界质量对应于Pg正好等于Pd时的质量,换言之
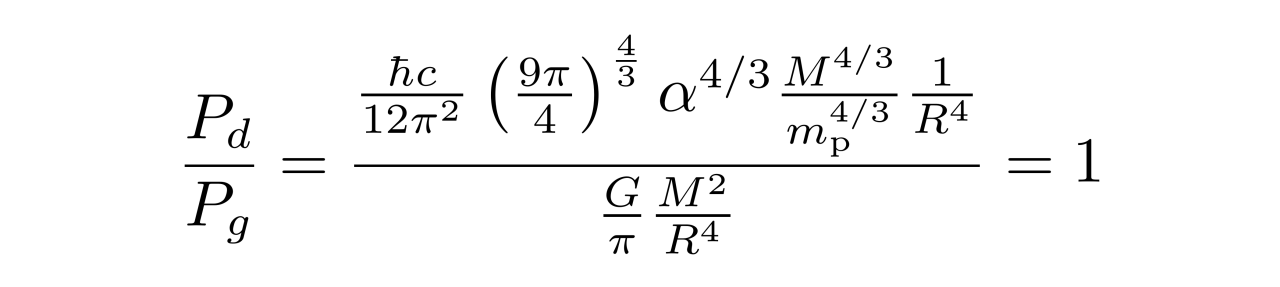
由此可以得到临界质量满足
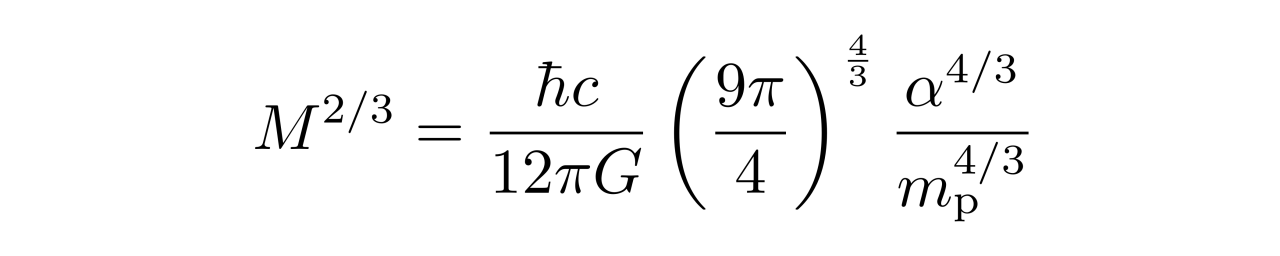
 (张朝阳计算极端相对论性电子气体简并压及白矮星极限质量)
(张朝阳计算极端相对论性电子气体简并压及白矮星极限质量)
代入相关数值,可得
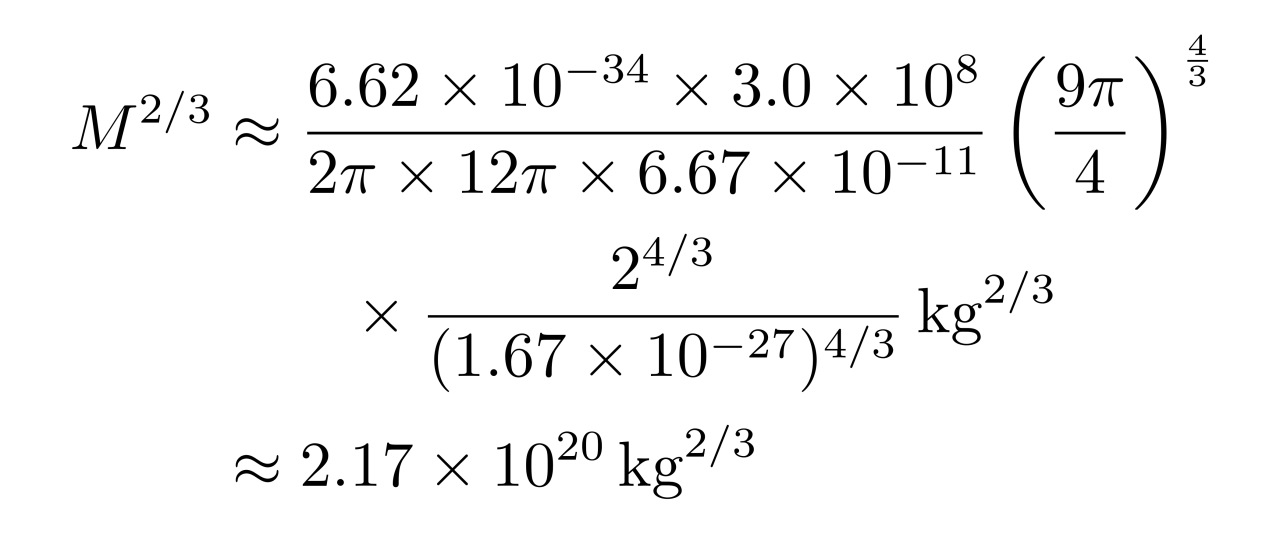
所以
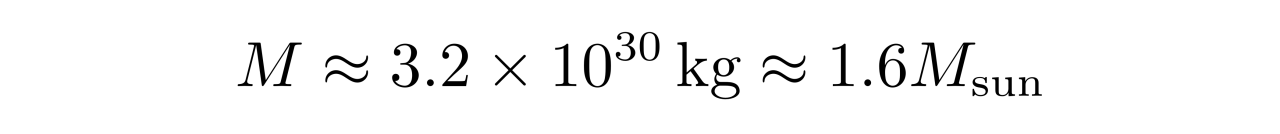
这就是白矮星的质量上限,大约是1.6倍的太阳质量。当然,这里的结果是近似得到的,因此与实际结果(1.44倍)存在一点差异。
据了解,《张朝阳的物理课》于每周五、周日中午12时在搜狐视频直播,网友可以在搜狐视频APP“关注流”中搜索“张朝阳”,观看直播及往期完整视频回放;关注“张朝阳的物理课”账号,查看课程中的“知识点”短视频;此外,还可以在搜狐新闻APP的“搜狐科技”账号上,阅览每期物理课程的详细文章。
